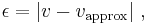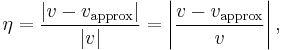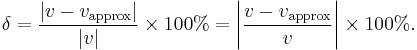Approximation error

The approximation error in some data is the discrepancy between an exact value and some approximation to it. An approximation error can occur because

  1. the measurement of the data is not precise due to the instruments. (e.g., the accurate reading of a piece of paper is 4.5cm but since the ruler does not use decimals, you round it to 5cm.) or
  2. approximations are used instead of the real data (e.g., 3.14 instead of π).

In the mathematical field of numerical analysis, the numerical stability of an algorithm in numerical analysis indicates how the error is propagated by the algorithm.

Contents

Overview

One commonly distinguishes between the relative error and the absolute error. The absolute error is the magnitude of the difference between the exact value and the approximation. The relative error is the absolute error divided by the magnitude of the exact value. The percent error is the relative error expressed in terms of per 100.

As an example, if the exact value is 50 and the approximation is 49.9, then the absolute error is 0.1 and the relative error is 0.1/50 = 0.002. The relative error is often used to compare approximations of numbers of widely differing size; for example, approximating the number 1,000 with an absolute error of 3 is, in most applications, much worse than approximating the number 1,000,000 with an absolute error of 3; in the first case the relative error is 0.003 and in the second it is only 0.000003.

Another example would be if you measured a beaker and read, 5mL. The correct reading would have been 6mL. This means that your % error (Approximate error) would be 16.66666.. % error.

Definitions

Given some value v and its approximation vapprox, the absolute error is

\epsilon = |v-v_\text{approx}|\ ,

where the vertical bars denote the absolute value. If :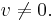v\ne 0. the relative error is

\eta = \frac{|v-v_\text{approx}|}{|v|} = \left| \frac{v-v_\text{approx}}{v} \right|,

and the percent error is

\delta = \frac{|v-v_\text{approx}|}{|v|}\times 100% = \left| \frac{v-v_\text{approx}}{v} \right|\times 100%.

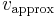These definitions can be extended to the case when v and v_{\text{approx}} are n-dimensional vectors, by replacing the absolute value with an n-norm.[1]

Instruments

In most indicating instruments, the accuracy is guaranteed to a certain percentage of full-scale reading. The limits of these deviations from the specified values are known as limiting errors or guarantee errors.[2]

See also

References

  1. ^ Golub, Gene; Charles F. Van Loan (1996). Matrix Computations – Third Edition. Baltimore: The Johns Hopkins University Press. pp. 53. ISBN 0-8018-5413-X. 
  2. ^ Albert D. Helfrick, Modern Electronic Instrumentation and Measurement Techniques, pg16, ISBN 81-297-0731-4

External links